
Simple rules and feedback for which complexity spontaneously emerges.
Edward Lorenz, from the Massachusetts Institute of Technology (MIT) is the official discoverer of chaos theory. He first observed the phenomenon as early as 1961 and, as a matter of irony, he discovered by chance what would be called later the chaos theory, in 1963 while making calculations with uncontrolled approximations aiming at predicting the weather.
Examples of progress leading to the understanding:
—— The Alan Turning Morphogenesis equations
—— Boris Belousov – Zhabotinsky (BZ) reaction of self organizing chemicals
—— The Mandelbrot set, quadratic recurrence equation:
Zn+1 = Z^2 + C or simply Z= Z^2 + C
Examples
It takes just 20 unaided generations to turn a simple computer feedback algorithm simulating human behavior into a true functioning process.
Mathematical chaos has been a hot topic in recent years. If you have seen Jurassic Park, you probably know a little about it already. Chaos is a property of some deterministic systems. A deterministic system is one in which future states depend strictly on the current conditions. They can be modeled by dynamical systems. Historically the idea has been that all processes occurring in the universe are deterministic, and that if we knew enough of the rules governing the behavior of the universe and had measurements about its current state we could predict what would happen in the future. These ideas have been applied with a great deal of success to falling objects, tide prediction, and many other systems. However, there have always been things which we have never been able to predict, things such as the weather. This was written off for a long time as being due to our incomplete knowledge of the system. With the development of chaos however, a new idea has emerged.
The essence of chaos is something called sensitive dependence on initial conditions. For the systems in which our ability to make predictions has been good, only a reasonable approximation of the initial state is necessary for prediction. The paths, or orbits, of initial conditions which are nearby to one another stay close together. A reasonable approximation of the current state yields a reasonable approximation of the future state. With sensitive dependence, this is not the case. In a system which exhibits sensitive dependence on initial conditions, reasonable approximations of the initial state do not provide reasonable approximations of the future state. The orbits of nearby initial conditions diverge until one can no longer discern any indication that they were once similar to one another. In order to make useful long term predictions in such a system, one needs measurements of initial conditions with infinite accuracy, which are impossible to obtain. This means that systems with a deterministic underpinning can generate behavior which seems random and unpredictable. A good example of such a system is the logistic map
The idea of deterministic chaos did not come to full fruition until after the advent of the computer, which could be used to model systems which were previously unapproachable by traditional methods. One of the most common methods of modelling a system is by way of a phase space diagram. A phase space diagram is a diagram created by plotting the various dependent variables of a system against one another. For example, one could create a phase space diagram by plotting a moving object’s position versus its velocity in two dimensions, or even by plotting its position vs. velocity vs. acceleration in three dimensions. The end result is something that looks like a single point moving along a path through space (this is the orbit that I spoke of earlier). This orbit can do several things: it can settle down to one point and stop, it can travel around in a circle, it can exhibit behavior which is predictable but not quite repetitive. It can also behave chaotically by traveling unpredictably on a path within a certain region of space, known as a chaotic attractor. Chaotic attractors can take may forms, but they all fall into a category of objects known as fractals.
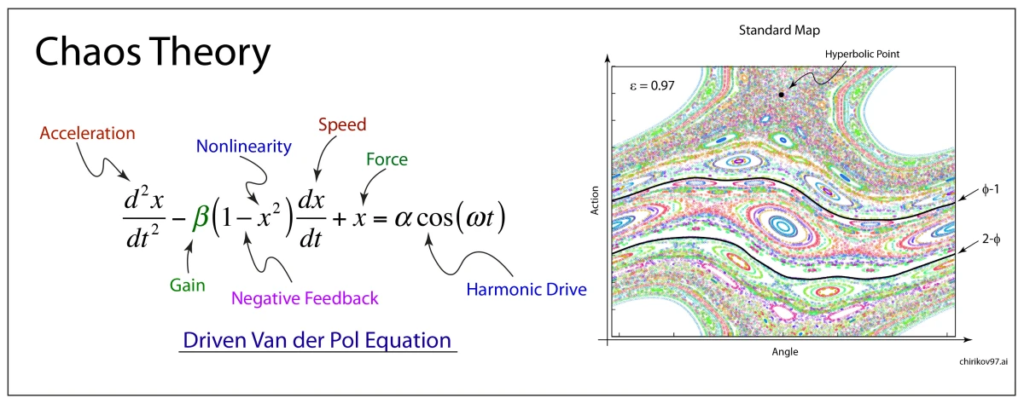
Research on the radar magnetron led to theoretical work on driven nonlinear oscillators,
including the discovery that a driven van der Pol oscillator could break up into wild and intermittent patterns.
This “bad” behavior of the oscillator circuit (bad for radar applications) was the first discovery of chaotic behavior in man-made circuits.
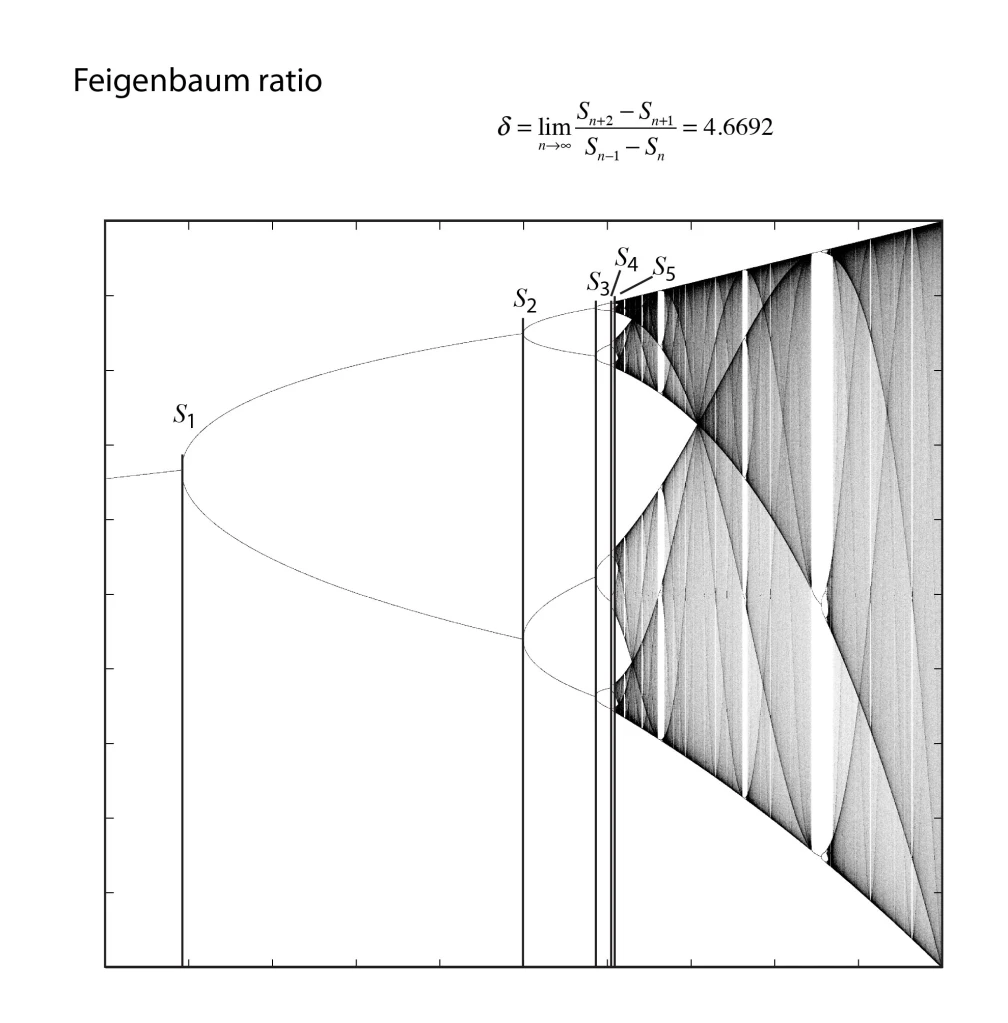
In 1976, computers were not common research tools, although hand-held calculators now were. One of the most famous of this era was the Hewlett-Packard HP-65, and Feigenbaum pushed it to its limits. He was particularly interested in the bifurcation cascade of the logistic map the way that bifurcations piled on top of bifurcations in a forking structure that showed increasing detail at increasingly fine scales. Feigenbaum was, after all, a high-energy theorist and had overlapped at Cornell with Kenneth Wilson when he was completing his seminal work on the renormalization group approach to scaling phenomena. Feigenbaum recognized a strong similarity between the bifurcation cascade and the ideas of real-space renormalization where smaller and smaller boxes were used to divide up space.
One of the key steps in the renormalization procedure was the need to identify a ratio of the sizes of smaller structures to larger structures. Feigenbaum began by studying how the bifurcations depended on the increasing growth rate. He calculated the threshold values rm for each of the bifurcations, and then took the ratios of the intervals, comparing the previous interval (rm-1 – rm-2) to the next interval (rm – rm-1). This procedure is like the well-known method to calculate the golden ratio = 1.61803 from the Fibonacci series, and Feigenbaum might have expected the golden ratio to emerge from his analysis of the logistic map. After all, the golden ratio has a scary habit of showing up in physics, just like in the KAM theory. However, as the bifurcation index m increased in Feigenbaum’s study, this ratio settled down to a limiting value of 4.66920. Then he did what anyone would do with an unfamiliar number that emerges from a physical calculation—he tried to see if it was a combination of other fundamental numbers, like pi and Euler’s constant e, and even the golden ratio. But none of these worked. He had found a new number that had universal application to chaos theory.
[ 4.6692 ]